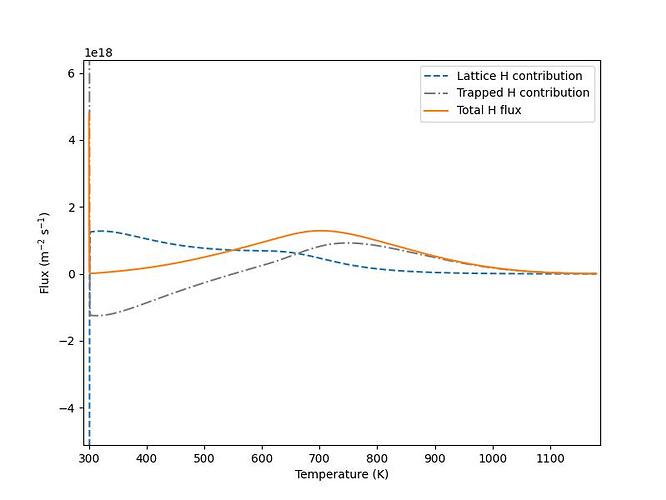
Hi all,
I am using FESTIM to fit a TDS curve to experimental data. Overall, the fit is fantastic and matches my experiments. However, when I look at the contribution of lattice H and trapped H, I see that in the beginning of the simulation, there is an initial spike in trapped H that is several orders of magnitude higher than the maximum desorption peak. This spike is offset by lattice H, resulting in a flux that is nearly 0.
What could be the reason for this spike in H flux? I suspect that it has to do with the inital condition or boundary condition I set. Diffusivity in this material is quite low, so I’m not expecting any significant detrapping to occur at room temperature.
This is my code:
import numpy as np
import matplotlib.pyplot as plt
import festim as F
import warnings
warnings.filterwarnings("ignore")
ni_atom_density = 9.140308E+28 # atoms/m^3 for nickel
eV = 96485 # eV to J conversion factor
a_IN718 = 3.591e-10 # lattice parameter of IN718 in m
thickness = 2.5e-4 # sample thickness in m
TDS_time=1760
def TDS(n1, E_p1):
trap_conc1 = n1 * ni_atom_density
simulation = F.Simulation()
nickel = F.Material(
id=1,
D_0=4.06e-7, # Diffusion frequency factor (m^2/s)
E_D=48630.5 / eV, # Diffusion activation energy in eV
)
simulation.materials = nickel
vertices = np.linspace(0, thickness, num=200)
simulation.mesh = F.MeshFromVertices(vertices)
trap_1 = F.Trap(
k_0=nickel.D_0 / ((2**0.5 / 2 * a_IN718)**2 * ni_atom_density),
E_k=nickel.E_D,
p_0=1.77e6,
E_p=E_p1,
density=trap_conc1,
materials=nickel,
)
simulation.traps = [trap_1]
simulation.initial_conditions = [
F.InitialCondition(field="1", value=trap_conc1),
]
simulation.boundary_conditions = [
F.DirichletBC(surfaces=[1, 2], value=0, field=0),
]
ramp = 0.5 # K/s
simulation.T = 300 + ramp * (F.t)
simulation.dt = F.Stepsize(
initial_value=0.1,
stepsize_change_ratio=1.2,
max_stepsize=lambda t: None if t < 1 else 2,
dt_min=1e-8,
)
simulation.settings = F.Settings(
absolute_tolerance=1e10,
relative_tolerance=1e-10,
final_time=TDS_time,
maximum_iterations=100,
)
derived_quantities = F.DerivedQuantities([
F.HydrogenFlux(surface=1),
F.HydrogenFlux(surface=2),
F.AverageVolume(field="T", volume=1),
F.TotalVolume(field="0", volume=1), # mobile (lattice) H
F.TotalVolume(field="1", volume=1) # trapped H
])
simulation.exports = [derived_quantities]
simulation.initialise()
simulation.run()
return derived_quantities
initial_guess = [4.08967605e-05, 3.41682841e-01]
res = TDS(*initial_guess)
T_data = np.array(res.filter(fields="T").data)
t_data = res.t
lattice_data = np.array(res.filter(fields="0").data)
trapped_data = np.array(res.filter(fields="1").data)
lattice_flux = -np.diff(lattice_data) / np.diff(t_data)
trapped_flux = -np.diff(trapped_data) / np.diff(t_data)
total_flux = lattice_flux + trapped_flux
plt.figure(figsize=(8, 6))
plt.plot(T_data[1:], lattice_flux, label="Lattice H contribution", linestyle="--")
plt.plot(T_data[1:], trapped_flux, label="Trapped H contribution", linestyle="-.",color="grey")
plt.plot(T_data[1:], total_flux, label="Total H flux")
plt.xlabel("Temperature (K)")
plt.ylabel("Flux (m$^{-2}$ s$^{-1}$)")
plt.legend()
plt.show()
Thank you for your help!