A series of simulations from plasma irradiation experiments to TDS

iamryo · July 25, 2024, 11:11am

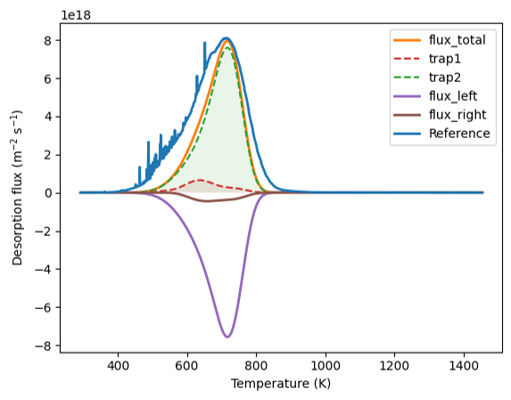
Hi everyone, I am trying to reproduce a series of plasma irradiation experiments on tungsten and TDS.(The goal is to reproduce the TDS spectrum.)
I am trying to reproduce a series of plasma irradiation and TDS with reference to Example 2 of the workshop.
However, I have some problems.

(1) When the value of E_p is reduced and the position of the peak is moved to the lower temperature side, the size of the peak should also be reduced.(I want to move the peak position without changing the peak size.)
To solve this problem, I tried changing the density of defects, but it did not work.

(2) I tried to write an auto-fitting code based on example 10 in the workshop. However, this also does not seem to work.

The experiment scenario is as follows.
The process is

\begin{equation} \begin{cases} \text{Implantation}, & \text{if} \: t < 3260 \\ \text{Cooling}, & \text{elif} \: 3260 <= t < 3295 \\ \text{Resting}, & \text{elif} \: 3295 <= t < 10460 \\ \text{TDS (1K/s)}, & \text{else} \: 10460 <= t < 11620 \\ \end{cases} \end{equation}

And the specimen temperature is

\begin{equation} T(t) = \begin{cases} 644, & \text{if} \: t < 3260 \\ 644-10(t-3260), & \text{elif} \: 3260 <= t < 3295 \\ 294, & \text{elif} \: 3295 <= t < 10460 \\ 294+(t-10460), & \text{else} \: 10460 <= t < 11620 \\ \end{cases} \end{equation}

T is expressed in \text{K}.

Implantation flux is

\begin{equation} \begin{cases} (1-r)6.1 \times 10^{21}\: \mathrm{D\:s^{-1}m^{-2}}, & \text{if} \: t < 3260 \\ 0, & \text{else}\\ \end{cases} \end{equation}

Then, r is reflectance

Implantation fluence is 2 \times 10^{25} \: \mathrm{D/m^2}.
and, Sample thickness is 0.2 \: \mathrm{mm}.

The code is shown below. Also. I also share the CSV of the reference data that is the subject of the reproduction.

TDS model

import festim as F
import numpy as np
import sympy as sp
import h_transport_materials as htm

import warnings

warnings.filterwarnings("ignore", category=DeprecationWarning)


def TDS(n1, E_p1, n2, E_p2):

    w_atom_density = 6.3e28  # atom/m3
    trap_conc1 = n1 * w_atom_density
    trap_conc2 = n2 * w_atom_density
    D = (htm.diffusivities.filter(material="tungsten").filter(author="frauenfelder")[0])

    # Define Simulation object
    synthetic_TDS = F.Simulation()

    # Define a simple mesh
    vertices=np.linspace(0, 0.2e-3, num=1000)
    synthetic_TDS.mesh = F.MeshFromVertices(vertices)

    # Define material properties
    tungsten = F.Material(
        id=1,
        D_0=D.pre_exp.magnitude,  # m2/s
        E_D=D.act_energy.magnitude,  # eV
    )
    synthetic_TDS.materials = tungsten

    # Define traps
    trap_1 = F.Trap(
        k_0=D.pre_exp.magnitude / (1.1e-10**2 * 6 * w_atom_density),
        E_k=D.act_energy.magnitude,
        p_0=1e13,
        E_p=E_p1,
        density=trap_conc1,
        materials=tungsten,
    )

    trap_2 = F.Trap(
        k_0=D.pre_exp.magnitude / (1.1e-10**2 * 6 * w_atom_density),
        E_k=D.act_energy.magnitude,
        p_0=1e13,
        E_p=E_p2,
        density=trap_conc2,
        materials=tungsten,
    )

    synthetic_TDS.traps = [trap_1, trap_2]

    # Set initial conditions
    implantation_time = 3260  # s
    r = 0.5
    ion_flux = sp.Piecewise(((1-r)*6.1e21, F.t <= implantation_time), (0, True))

    # Set boundary conditions
    synthetic_TDS.boundary_conditions = [
        F.ImplantationDirichlet(surfaces=1, phi=ion_flux, R_p=4.5e-9, D_0=D.pre_exp.magnitude, E_D=D.act_energy.magnitude),
        F.DirichletBC(surfaces=2, value=0, field=0)
    ]

    # Define the material temperature evolution
    implantation_temp = 644  # K
    temperature_ramp = 1  # K/s
    cooling_ramp = 10  # K/s
    cooling_time = 350/cooling_ramp
    
    start_tds = implantation_time + 7200  # s
    
    synthetic_TDS.T = F.Temperature(
        value=sp.Piecewise(
            (implantation_temp, F.t < implantation_time),
            (implantation_temp - cooling_ramp*(F.t-implantation_time), (implantation_time <= F.t)&(F.t < implantation_time+cooling_time)),
            (implantation_temp - cooling_ramp*(implantation_time+cooling_time-implantation_time), (implantation_time+cooling_time <= F.t)&(F.t < start_tds)),
            (implantation_temp - cooling_ramp*(implantation_time+cooling_time-implantation_time) + temperature_ramp*(F.t-start_tds), True),
        )
    )

    # Define the simulation settings
    synthetic_TDS.dt = F.Stepsize(
        initial_value=0.01,
        stepsize_change_ratio=1.2,
        max_stepsize=lambda t: 5 if t >= start_tds else None,
        dt_min=1e-08,
        milestones=[implantation_time, start_tds],
    )

    synthetic_TDS.settings = F.Settings(
        absolute_tolerance=1e11,
        relative_tolerance=1e-10,
        final_time=11620,
        maximum_iterations=50,
    )

    # Define the exports
    derived_quantities = F.DerivedQuantities(
        [
            F.TotalVolume("solute", volume=1),
            F.TotalVolume("retention", volume=1),
            F.TotalVolume("1", volume=1),
            F.TotalVolume("2", volume=1),
            F.HydrogenFlux(surface=1),
            F.HydrogenFlux(surface=2),
            F.AverageVolume(field="T", volume=1)
        ]
    )

    synthetic_TDS.exports = [derived_quantities]
    synthetic_TDS.initialise()
    synthetic_TDS.run()

    return derived_quantities

Generate dummy data

# Get the flux dependence
reference_prms = [8.0e-4, 0.85, 5.0e-4, 1.2]
data = TDS(*reference_prms)

Plot dummy data

import matplotlib.pyplot as plt
import os 

# Get temperature
T = data.filter(fields="T").data

# Calculate the total desorptio flux
flux_left = data.filter(fields="solute", surfaces=1).data
flux_right = data.filter(fields="solute", surfaces=2).data
flux_total = -(np.array(flux_left) + np.array(flux_right))

t = data.t
implantation_time = 3260  # s
start_tds = implantation_time + 7200  # s
tds_start_ind = t.index(start_tds)

T = T[tds_start_ind:]
flux_left = flux_left[tds_start_ind:]
flux_right = flux_right[tds_start_ind:]
flux_total = flux_total[tds_start_ind:]

trap_1 = data.filter(fields="1").data
trap_2 = data.filter(fields="2").data

contribution_trap_1 = -np.diff(trap_1)/np.diff(t)
contribution_trap_2 = -np.diff(trap_2)/np.diff(t)

contribution_trap_1 = contribution_trap_1[tds_start_ind-1:]
contribution_trap_2 = contribution_trap_2[tds_start_ind-1:]

# Visualise
plt.plot(T, flux_total, linewidth=2, label='flux_total')
plt.plot(T, contribution_trap_1, linestyle="--", color="red", label='trap1')
plt.fill_between(T, 0, contribution_trap_1, facecolor='red', alpha=0.1)
plt.plot(T, contribution_trap_2, linestyle="--", color="orange", label='trap2')
plt.fill_between(T, 0, contribution_trap_2, facecolor='orange', alpha=0.1)

plt.legend()
plt.ylabel(r"Desorption flux (m$^{-2}$ s$^{-1}$)")
plt.xlabel(r"Temperature (K)")
plt.show()

Automated TDS fit

ref = np.genfromtxt("tds-ref-fit.csv", delimiter=";")
ref[0][0]=ref[1][0]     # ref[0][0]=nan without this script.


def info(i, p):
    """
    Print information during the fitting procedure
    """
    print("-" * 40)
    print(f"i = {i}")
    print("New simulation.")
    print(f"Point is: {p}")

from scipy.interpolate import interp1d

prms = []
errors = []


def error_function(prm):
    """
    Compute average absolute error between simulation and reference
    """
    global i
    global prms
    global errors
    prms.append(prm)
    i += 1
    info(i, prm)

    # Filter the results if a negative value is found
    if any([e < 0 for e in prm]):
        return 1e30

    # Get the simulation result
    n1, Ep1, n2, Ep2 = prm
    res = TDS(n1, Ep1, n2, Ep2)

    implantation_time = 3260  # s
    start_tds = implantation_time + 7200  # s
    tds_start_ind = t.index(start_tds)

    T = np.array(res.filter(fields="T").data)
    T = T[tds_start_ind:]
    flux = -np.array(res.filter(fields="solute", surfaces=1).data) - np.array(
        res.filter(fields="solute", surfaces=2).data
    )
    flux = flux[tds_start_ind:]

    # Plot the intermediate TDS spectra
    if i == 1:
        plt.plot(T, flux, color="tab:red", lw=2, label="Initial guess")
    else:
        plt.plot(T, flux, color="tab:grey", lw=0.5)

    interp_tds = interp1d(T, flux, fill_value="extrapolate")

    # Compute the mean absolute error between sim and ref
    err = np.abs(interp_tds(ref[:, 0]) - ref[:, 1]).mean()

    print(f"Average absolute error is : {err:.2e}")
    errors.append(err)
    return err

from scipy.optimize import minimize

i = 0  # initialise counter

# Set the tolerances
fatol = 1e18
xatol = 1e-3

initial_guess = [8.0e-4, 0.85, 5.0e-4, 1.2]

# Minimise the error function
res = minimize(
    error_function,
    np.array(initial_guess),
    method="Nelder-Mead",
    options={"disp": True, "fatol": fatol, "xatol": xatol},
)

# Process the obtained results
predicted_data = TDS(*res.x)

T = predicted_data.filter(fields="T").data
T = T[tds_start_ind:]

flux_left = predicted_data.filter(fields="solute", surfaces=1).data
flux_right = predicted_data.filter(fields="solute", surfaces=2).data
flux_total = -(np.array(flux_left) + np.array(flux_right))
flux_total = flux_total[tds_start_ind:]

# Visualise
plt.plot(ref[:, 0], ref[:, 1], linewidth=2, label="Reference")
plt.plot(T, flux_total, linewidth=2, label="Optimised")

plt.ylabel(r"Desorption flux (m$^{-2}$ s$^{-1}$)")
plt.xlabel(r"Temperature (K)")
plt.legend()
plt.show()

Thank you very much if someone has an idea.

remidm · July 25, 2024, 12:21pm

Hi @iamryo and welcome!

Do you expect peaks below the implantation temperature (here 644 K)?

remidm · July 25, 2024, 12:25pm

I was able to get a better fit (although far from perfect) with these parameters

initial_guess = [20 * 8.0e-4, 0.85, 25 * 5.0e-4, 1.12]

You may want to try and plot the contributions to the computed spectrum of:

each trap
each surface (left and right)

I suspect that here, trap1 has little to no influence on the TDS spectrum because its detrapping energy is too low compared to the implantation temperature.

iamryo · July 25, 2024, 1:23pm

Hi @remidm and thank you for your replying!

From the reference TDS spectrum, I see peaks around 550 K and 700 K, so I think the 550 K peak is below the injection temperature (644 K).
However, this sample have blistering and I think the 550 K peak is due to those bursting (based on the spikes in the TDS spectrum, I think so).
Thus, if I can reproduce the 700 K peak by FESTIM, I would be satisfied.

By the way, is it physically strange to see peaks at temperatures lower than the implantation temperature?

remidm · July 25, 2024, 2:45pm

well then I think that you can keep this model and tweak the parameters a bit more (cf the fit I sent) to fit your 700 K peak

In that case then you may need different mathematical models for describing these bursts. Maybe someone in the FESTIM community has more experience with that. You could send a message in the FESTIM Slack

I wouldn’t say physically strange (there could be other models explaining this than “classical” traps) but it’s unusual, yes.
This is because during the implantation at say 600K, if a trap has a “detrapping temperature” (related to its detrapping energy) below 600K then it will remain empty as the detrapping rate will be much higher than the trapping rate. So this trap cannot contribute to the TDS spectrum.

Then again you could have low temperature peaks due to mobile (untrapped) hydrogen still present in the sample after the resting period (between the implantation and TDS) desorbing at the beginning of the TDS.

Maybe @ehodille can comment too

remidm · July 25, 2024, 3:02pm

Other things to consider:

are you certain that your traps are homogeneously distributed in your sample?
do you have profilometry data that you could use to constrain your fit a bit more?
do you know if you are creating defects during the plasma irradiation?
have you checked that the experimental time evolution of the temperature matches the temperature evolution of your FESTIM model? Differences in the temperature ramp/evolution can affect the TDS spectrum

iamryo · July 26, 2024, 12:09pm

Thank you so much for your detailed explanation.

I’m not certain that my traps are homogeneously distributed in my sample.
However, I think that the distribution is basically homogeneous since the specimen is not treated in any way that would cause damage before plasma implantation.

On the other hand, I think the fact that defects (blistering) were created during plasma implantation needs to be take into the simulation.

Now, I have rewritten the code to reflect your comments.
The rewritten contents are,

The temperature evolution is matched to that of the experiment.
I have restricted the density of Trap2 to near the surface (<10e-6). I think this area has a blistering effect from FIB-SEM images of the reference sample.

As a result, the following spectra were obtained.
The position of the peak was aligned with the reference.
fit-3

this work does not take into account the time evolution of defects due to plasma irradiation.
So in the next step, I would try to do this.

remidm · July 26, 2024, 2:18pm

Glad to see the fit is better now.

I think having NRA profiles or some kind of profilometry is really important to lift this uncertainty.

The physics of blistering and bursting is not trivial and this is more a research problem than a FESTIM problem

We discussed recently how to include experimental data for temperature.

What is the energy of the ions?

iamryo · July 30, 2024, 1:41am

NRA is one of the things I would like to do. To tell the truth, the price (too expensive) and the lack of available facilities nearby are the main obstacles…

I would like to send a message about the reproduction of TDS spectra with blistering on Slack. Do I just post it somewhere on an existing channel?

Thank you. I’ll take a look.

It’s 25 eV.

remidm · July 30, 2024, 7:01am

Sure feel free to send a message on the general channel on Slack

Topic		Replies	Views
Second peak in TDS simulation for a single trap User Support	5	71	May 27, 2024
Simulation doesn't converge under local traps condition User Support	3	36	March 10, 2025
Understanding depth profiles User Support	6	74	February 20, 2025
Zero flux in plasma implantion and TDS User Support	3	23	August 4, 2025
Spike in trapped H at low temperature in TDS simulation User Support	5	36	March 17, 2025

A series of simulations from plasma irradiation experiments to TDS

TDS model

Generate dummy data

Plot dummy data

Automated TDS fit

Related topics