Point is not inside the domain when exporting surface flux

Ucempvs · March 24, 2025, 7:37am

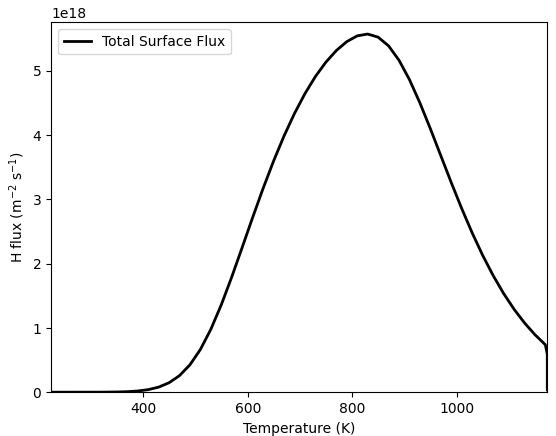
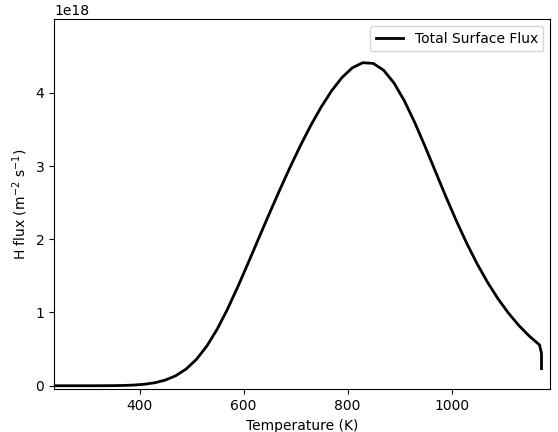
Hello all,

I want to perform a simulation on a 3D disc-shaped structure that I meshed with SALOME and then export the surface flux as a derived quantity. However, I noticed that when I use a finer mesh, I get the error message

 File "/home/ucempvs/FESTIM/Disc/CAD_example.py", line 116, in <module>
    preview_plot(5.10924409e-04, 0.21747223 )
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  File "/home/ucempvs/FESTIM/Disc/CAD_example.py", line 108, in preview_plot
    res = TDS(*prm)
  File "/home/ucempvs/FESTIM/Disc/CAD_example.py", line 101, in TDS
    simulation.run()
    ~~~~~~~~~~~~~~^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/generic_simulation.py", line 460, in
 run
    self.run_transient()
    ~~~~~~~~~~~~~~~~~~^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/generic_simulation.py", line 483, in
 run_transient
    self.iterate()
    ~~~~~~~~~~~~^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/generic_simulation.py", line 517, in
 iterate
    self.run_post_processing()
    ~~~~~~~~~~~~~~~~~~~~~~~~^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/generic_simulation.py", line 544, in
 run_post_processing
    self.exports.write(
    ~~~~~~~~~~~~~~~~~~^
        self.label_to_function,
        ^^^^^^^^^^^^^^^^^^^^^^^
        self.mesh.dx,
        ^^^^^^^^^^^^^
    )
    ^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/exports/exports.py", line 77, in write
    export.compute(self.t)
    ~~~~~~~~~~~~~~^^^^^^^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/exports/derived_quantities/derived_quantities.py", line 133, in compute
    value = quantity.compute()
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/exports/derived_quantities/surface_flux.py", line 77, in compute
    flux = f.assemble(
        self.prop * f.dot(f.grad(self.function), self.n) * self.ds(self.surface)
    )
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/dolfin/fem/assembling.py", line 213, in assemble
    assembler.assemble(tensor, dolfin_form)
    ~~~~~~~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/dolfin/function/expression.py", line 56, in
 wrapped_eval_cell
    self.user_expression.eval_cell(values, x, cell)
    ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~^^^^^^^^^^^^^^^^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/festim/materials/materials.py", line 363, in eval_cell
    value[0] = D_0 * f.exp(-E_D / k_B / self._T(x))
                                        ~~~~~~~^^^
  File "/home/ucempvs/anaconda3/envs/festim-env/lib/python3.13/site-packages/dolfin/function/function.py", line 337, in __call__
    self._cpp_object.eval(values, x)
    ~~~~~~~~~~~~~~~~~~~~~^^^^^^^^^^^
RuntimeError:


*** -------------------------------------------------------------------------
*** DOLFIN encountered an error. If you are not able to resolve this issue
*** using the information listed below, you can ask for help at
***
***     fenics-support@googlegroups.com
***
*** Remember to include the error message listed below and, if possible,
*** include a *minimal* running example to reproduce the error.
***
*** -------------------------------------------------------------------------
*** Error:   Unable to evaluate function at point.
*** Reason:  The point is not inside the domain. Consider calling "Function::set_allow_extrapolation(true)" on this Function to allow extrapolation.
*** Where:   This error was encountered inside Function.cpp.
*** Process: 0
***
*** DOLFIN version: 2019.1.0
*** Git changeset:  e7ee545889ccbd48d64c71286627e7f8ae60a690
*** -------------------------------------------------------------------------

Exporting to XDMF works as expected and when I remove the surface flux from the list of derived quantities, the code also runs.

Here is my code:

import matplotlib.pyplot as plt
import festim as F
import numpy as np
import warnings

warnings.filterwarnings("ignore", category=DeprecationWarning)

ni_atom_density = 9.140308E+28  
eV = 96485  # eV to J conversion factor
a_IN718 = 3.591e-10 #lattice parameter of IN718 in m

id_vol = 9

id_top = 6
id_bottom = 7
id_rim = 8


def TDS(n1, E_p1):
 
    trap_conc1 = n1 * ni_atom_density   #sites/m3

    simulation = F.Simulation()
    #simulation.log_level = 20

    simulation.mesh = F.MeshFromXDMF(volume_file="Disc/Mesh/mesh_domains.xdmf", boundary_file="Disc/Mesh/mesh_boundaries.xdmf")

    IN718 = F.Material(
        id=id_vol,   #ID from mesh file
        D_0=4.06e-7,         # Diffusion frequency factor (m^2/s)
        E_D=48630.5 / eV,     # Diffusion activation energy in eV
    )
    
    simulation.materials = IN718

    # Define trap properties
    trap_1 = F.Trap(
        k_0=IN718.D_0 /((2**0.5/2*a_IN718)**2*ni_atom_density),
        E_k=IN718.E_D,
        p_0=1.77e6, 
	    E_p=E_p1,
        density=trap_conc1,
        materials=IN718,
    )

    simulation.traps = [trap_1]

    simulation.initial_conditions = [      
        F.InitialCondition(field="1", value = trap_conc1,label=id_vol), 
        ]

    simulation.boundary_conditions = [
        F.DirichletBC(surfaces=[id_top, id_bottom, id_rim], value=0, field=0),
    ]

    ramp = 0.5  # K/s

    simulation.T = 200 + ramp * (F.t)


    simulation.dt = F.Stepsize(
        initial_value=0.1,
        stepsize_change_ratio=1.2,
        max_stepsize=lambda t: None if t < 1 else 2,
        dt_min=1e-8,
    )

    simulation.settings = F.Settings(
        absolute_tolerance=1e11,
        relative_tolerance=1e-6,
        final_time=2500,
        maximum_iterations=100,
    )

    export_folder = "TDS_Fit_Exports/Disc_No_Oxide_1_Trap"

    derived_quantities = F.DerivedQuantities(
        [
            F.SurfaceFlux(field="solute",surface=id_top),
            F.AverageVolume(field="T", volume=id_vol), #temperature
            F.TotalVolume(field="0", volume=id_vol), #mobile H   
            F.AverageVolume(field="0", volume=id_vol), #exports volume of mobile H in H/m3 for solute H 
            F.TotalVolume(field="1", volume=id_vol),  
            F.AverageVolume(field="1", volume=id_vol),          
        ],
        show_units=True,
    )

    xdmf_exports = [
        F.XDMFExport(field="T", filename=export_folder + "/T.xdmf", checkpoint=False),
        F.XDMFExport(field="0", filename=export_folder + "/Mobile H.xdmf", checkpoint=False),
        F.XDMFExport(field="1", filename=export_folder + "/Trapped H.xdmf", checkpoint=False),
    ]
     
    simulation.exports = [derived_quantities] + xdmf_exports

    simulation.initialise()
    simulation.run()


    return derived_quantities


def preview_plot(*prm):
    res = TDS(*prm)
    
    T = np.array(res.filter(fields="T").data)
    flux = -np.array(res[0].data)
    plt.plot(T, flux, linewidth=2, color="black")
    plt.show()
     

preview_plot(5.10924409e-04, 0.21747223 )

The mesh was created in SALOME and converted to XDMF using the code in the workshop task 8:

import meshio


def convert_med_to_xdmf(
    med_file,
    cell_file="mesh_domains.xdmf",
    facet_file="mesh_boundaries.xdmf",
    cell_type="tetra",
    facet_type="triangle",
):
    """Converts a MED mesh to XDMF
    Args:
        med_file (str): the name of the MED file
        cell_file (str, optional): the name of the file containing the
            volume markers. Defaults to "mesh_domains.xdmf".
        facet_file (str, optional): the name of the file containing the
            surface markers.. Defaults to "mesh_boundaries.xdmf".
        cell_type (str, optional): The topology of the cells. Defaults to "tetra".
        facet_type (str, optional): The topology of the facets. Defaults to "triangle".
    Returns:
        dict, dict: the correspondance dict, the cell types
    """
    msh = meshio.read(med_file)

    correspondance_dict = msh.cell_tags

    cell_data_types = msh.cell_data_dict["cell_tags"].keys()

    for mesh_block in msh.cells:
        if mesh_block.type == cell_type:

            meshio.write_points_cells(
                cell_file,
                msh.points,
                [mesh_block],
                cell_data={"f": [-1 * msh.cell_data_dict["cell_tags"][cell_type]]},
            )
        elif mesh_block.type == facet_type:
            meshio.write_points_cells(
                facet_file,
                msh.points,
                [mesh_block],
                cell_data={"f": [-1 * msh.cell_data_dict["cell_tags"][facet_type]]},
            )

    return correspondance_dict, cell_data_types


correspondance_dict, cell_data_types = convert_med_to_xdmf("Disc/Mesh/Disc.med", cell_file="mesh_domains.xdmf", facet_file="mesh_boundaries.xdmf")

print(correspondance_dict)

I tried using different meshing algorithms in SALOME but to no avail…
Attached you can find one mesh where the simulation works as expected and one where it doesn’t.

Thank you for your help!

Mesh_Files.zip (435.1 KB)

remidm · March 24, 2025, 12:39pm

Hey @Ucempvs

Are you running this in parallel by any chance?

Ucempvs · March 24, 2025, 2:20pm

Hi Remi,

no, I’m not running in parallel.

remidm · March 24, 2025, 2:35pm

ok thanks, I’ll try to reproduce your error. In the meantime, I see that your file isn’t really a MWE (minimal reproducible example). For example, the XDMF exports aren’t needed, the TDS plot isn’t needed, etc. Also the mesh filenames don’t match the ones in your script, making it harder for me to reproduce your issue

remidm · March 24, 2025, 2:52pm

Been able to reproduce the issue with:

import festim as F

id_vol = 9

id_top = 6
id_bottom = 7
id_rim = 8


simulation = F.Simulation()
# simulation.log_level = 20

simulation.mesh = F.MeshFromXDMF(
    volume_file="mesh_domains.xdmf",
    boundary_file="mesh_boundaries.xdmf",
)

simulation.materials = F.Material(id=id_vol, D_0=1, E_D=0)

simulation.T = 300

simulation.dt = 0.1

simulation.settings = F.Settings(
    absolute_tolerance=1e11,
    relative_tolerance=1e-10,
    final_time=1,
)

derived_quantities = F.DerivedQuantities(
    [F.SurfaceFlux(field="solute", surface=id_top)],
    show_units=True,
)

simulation.exports = [derived_quantities]

simulation.initialise()
simulation.run()

remidm · March 24, 2025, 3:05pm

@Ucempvs looks to me like it’s a mesh-precision error, which would explain why you don’t have this bug on a finer mesh.

Been able to reproduce the error with a pure FEniCS example:

import fenics as f

mesh = f.Mesh()
f.XDMFFile("mesh_domains.xdmf").read(mesh)
V = f.FunctionSpace(mesh, "CG", 1)
u = f.Function(V)


class Diff(f.UserExpression):
    def eval_cell(self, value, x, ufc_cell):
        D_0 = 1
        E_D = 0.1
        k_B = 8.6173303e-5
        value[0] = D_0 * f.exp(-E_D / k_B / u(x))

    def value_shape(self):
        return ()


my_coeff = Diff()

n = f.FacetNormal(mesh)

flux = f.assemble(my_coeff * f.dot(f.grad(u), n) * f.ds)

remidm · March 24, 2025, 3:14pm

In the above example, setting

u.set_allow_extrapolation(True)

Seems to fix the issue.

Which means the MWE I provided above can be fixed with:

import festim as F

id_vol = 9

id_top = 6
id_bottom = 7
id_rim = 8


simulation = F.Simulation()
# simulation.log_level = 20

simulation.mesh = F.MeshFromXDMF(
    volume_file="mesh_domains.xdmf",
    boundary_file="mesh_boundaries.xdmf",
)

simulation.materials = F.Material(id=id_vol, D_0=1, E_D=0)

simulation.T = 300

simulation.dt = 0.1

simulation.settings = F.Settings(
    absolute_tolerance=1e11,
    relative_tolerance=1e-10,
    final_time=1,
)

derived_quantities = F.DerivedQuantities(
    [F.SurfaceFlux(field="solute", surface=id_bottom)],
    show_units=True,
)

simulation.exports = [derived_quantities]

simulation.initialise()

# after initialise, allow extrapolation of temeperature
simulation.T.T.set_allow_extrapolation(True)

simulation.run()

This makes this MWE run fine. However this looks a bit hacky so you may want to investigate these mesh inaccuracies. Have you considered using GMSH instead of SALOME?

Ucempvs · March 24, 2025, 3:45pm

Amazing, thank you for going through the effort of reproducing the issue and sorry about leaving some unnecessary stuff in the code.
I haven’t tried GMSH yet but can give it a go if you think it might prevent this issue!

remidm · March 24, 2025, 3:53pm

It’s definitely something to do with mesh precision. I must admit this doesn’t occur a lot… if ever… maybe there is a way to “clean” the mesh in SALOME? is it made of several volumes?

We have a tutorial with GMSH in the documentation written by @celyn

remidm · March 24, 2025, 3:57pm

Also, maybe moving to FESTIM2 could help? I believe all the functionality is already there to simulate this problem.

Ucempvs · March 25, 2025, 7:02am

oh is it? I was holding back from moving to FESTIM 2 but I might give it a go now!

VVKulagin · March 25, 2025, 8:00am

Hi @Ucempvs !

At first glance, your problem is axisymmetric. Did you consider solving your problem in cylindrical coordinates?

remidm · March 25, 2025, 12:29pm

Yes it can do trapping although the way we handle it changed slightly. It seems this is all you need.

To @VVKulagin 's comment, if your system is indeed axisymmetric you may want to run it in 2D-cylindrical to save up some computational resources.

FESTIM2 doesn’t handle cylindrical yet though

Ucempvs · March 25, 2025, 1:11pm

@VVKulagin, thank you for your suggestion, it is indeed axissymmetric. The only reason I went for the 3D simulation is that I need to consider H desorption from three sides (top, sides, bottom) of the disc as the thickness is quite large.
My understanding was that I can’t do that with cylindrical coordinates.

To be honest, for finding the initial trapping parameters, I am quite happy with computation time when I use a relatively coarse mesh (~3 minutes per iteration on my laptop).

remidm · March 25, 2025, 1:24pm

This is totally doable in 2D-cylindrical. On the following diagram, you simply set surfaces 1, 2, and 3 with c=0 and then set three different derived quantities.

Ucempvs · March 25, 2025, 7:06pm

Gave it a go and looks quite close to the results from the 3D simulation
2D:

3D:

There’s a discrepancy of ~1e18 in the H flux between 2D and 3D but I’m guessing that this could be a consequence of the coarser mesh for 3D simulations? Refining it seems to narrow the gap between the two.

If that’s the case then I’ll definitely stick with 2D

remidm · March 25, 2025, 7:31pm

Careful with the units here. Are you sure it’s H/m2/s and not H/s?

I would try and have either some local refinement near the surfaces or a finer mesh overall to avoid these oscillations (ref. 2D field).

Ucempvs · March 26, 2025, 6:35am

good shout!
The units should be right, I divided the flux by the respective surface areas to be able to compare it to experimental data

Topic		Replies	Views
Concentration is zero in some subdomains User Support	8	65	June 11, 2024
Tag the geometry with Salome User Support	4	43	May 24, 2024
Two Layered Monoblock User Support	8	49	July 24, 2024
Export point value User Support	2	25	July 22, 2024
Problems when reproducing the results of the article User Support	20	155	May 31, 2024

Point is not inside the domain when exporting surface flux

Related topics